Гармонический сигнал и его характеристики
Основная информация
Гармонические колебания — это особый тип механических или электромагнитных колебаний, которые описываются синусоидальными функциями. Они характеризуются периодическими изменениями величины во времени или в пространстве, где сила или воздействие пропорциональны отклонению от равновесия и направлены в противоположную сторону.
Одним из наиболее распространенных колебаний, используемых в радиотехнике, являются гармонические (синусоидальные) колебания. Давайте вспомним основные параметры, которые их характеризуют, а также способы их представления.
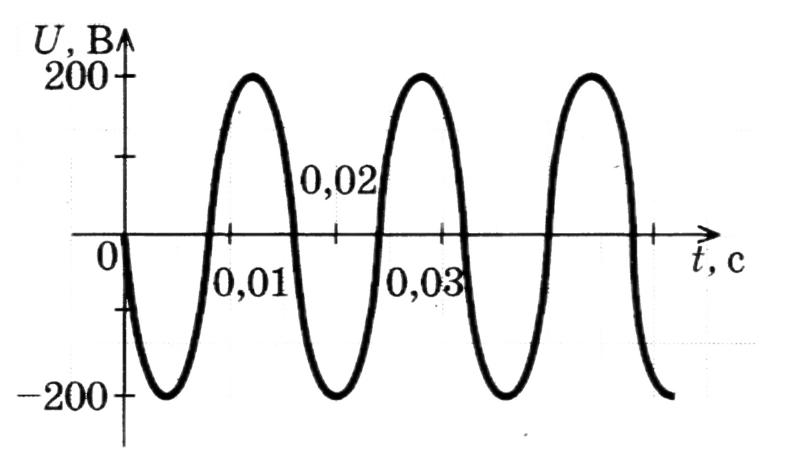
Для наглядности, на рисунке ниже показан график синусоидального напряжения, который обладает следующими параметрами:
- i(t) — мгновенное значение сигнала, которое определяет его амплитуду в любой момент времени и часто обозначается буквой «i.»
- U — амплитуда, представляющая максимальное отклонение колебаний от нулевой линии.
- T — период, то есть минимальное время, за которое сигнал завершает один полный цикл и возвращается к исходной фазе.
- f — частота, представляющая количество полных циклов колебаний в единицу времени (часто измеряется в герцах, 1 Гц = 1/с).
- φ — начальная фаза колебаний, которая определяет их положение относительно начального момента времени. Если мгновенное значение колебаний при t = 0 больше нуля, начальная фаза положительная (со знаком «+»), и наоборот, если меньше нуля, то начальная фаза отрицательная (со знаком «-«). Колебания с положительной начальной фазой называют опережающими, а с отрицательной — отстающими.
Гармонические колебания являются важными в радиотехнике и других областях, так как они могут использоваться для анализа и моделирования различных физических процессов и сигналов. Их математическое описание и понимание параметров помогают инженерам и ученым в создании и анализе радиотехнических систем и устройств.
Опережающие и запаздывающие колебания
Колебание с опережающей фазой
Колебание с опережающей фазой (положительной начальной фазой) — это такое колебание, в котором момент начала колебаний происходит раньше относительно определенной точки отсчета или эталона. В контексте синусоидальных колебаний, такое колебание начинает свое движение, достигая максимальной амплитуды или другой характерной точки, раньше, чем остальные колебания или эталон.
Колебание с отстающей фазой
Колебание с отстающей фазой (отрицательной начальной фазой) — это обратный случай. В этом колебании момент начала движения происходит позже относительно точки отсчета или эталона. Это означает, что пиковые значения колебания достигаются позже по времени, чем у других сигналов или эталона.
Для лучшего понимания можно представить две синусоидальные волны с одинаковой частотой. Если одна из них начинает свое колебание немного раньше (положительная начальная фаза), она опережает другую в терминах времени. Если она начинает свое колебание немного позже (отрицательная начальная фаза), она отстает от первой во времени.
Эти понятия фазы важны в радиоэлектронике и сигнальной обработке, поскольку они могут влиять на взаимодействие сигналов и точность синхронизации в различных устройствах и системах.
Форма временных колебаний
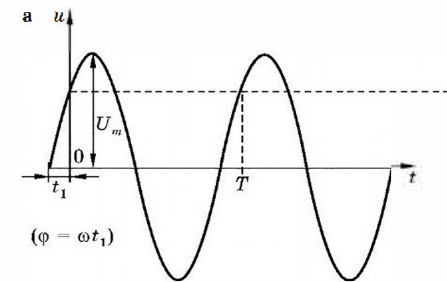
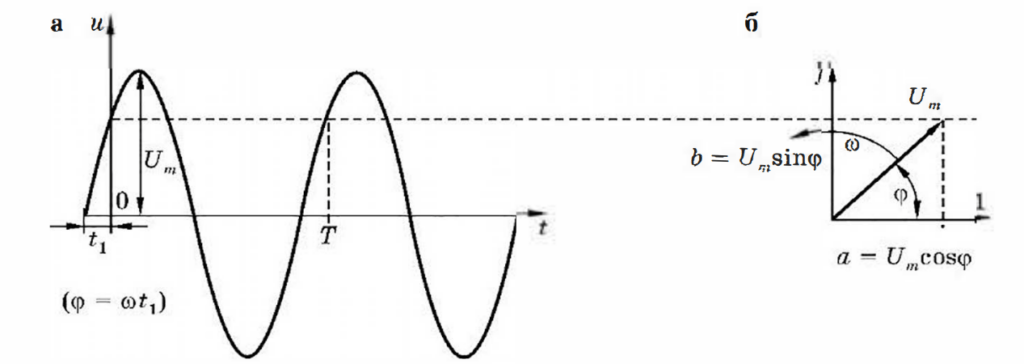
Приведенная на рисунке форма представления колебания называется временной, и ей соответствует математическая запись:
u(t)=Umsin(ωt+φ)
Однако при решении различных радиотехнических задач такая форма записи иногда оказывается громоздкой, затрудняющей не только решение, но и осознание происходящих физических процессов. В этих случаях для гармонического колебания используют другую форму представления сигнала, называемую векторной.
Векторная форма
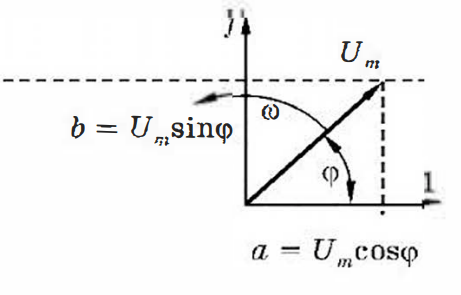
Векторная форма представления гармонических колебаний — это графический способ представления, который позволяет легче визуализировать, как происходят гармонические колебания. Вместо математических уравнений мы используем векторы и геометрические концепции. Вот как это работает:
- Вектор амплитуды (U): Вектор, представляющий амплитуду колебаний, изображает длину и направление колебаний. Его длина соответствует амплитуде сигнала.
- Угловая скорость (ω): Это параметр, который определяет, как быстро вектор амплитуды вращается. Чем выше частота сигнала, тем быстрее он вращается. Угол поворота вектора за единицу времени равен угловой скорости.
- Начальная фаза (φ): Начальная фаза определяет угол между вектором амплитуды и некоторой опорной осью в момент времени t = 0. Это означает, в какой точке начинается колебание.
Формула для представления гармонического колебания в векторной форме:
I(t)=U⋅sin(ωt+φ)
Где:
- I(t) — мгновенное значение гармонического колебания в момент времени t.
- U — амплитуда колебания, длина вектора амплитуды.
- ω — угловая скорость.
- φ — начальная фаза, угол, который определяет начальное положение вектора амплитуды в момент времени t=0.
Угловая скорость определяется:
ω=2πf
Представьте себе вектор амплитуды, начинающий свое вращение против часовой стрелки с заданной угловой скоростью. Начальная фаза определяет его начальное положение. Поворачиваясь, вектор создает гармонические колебания.
Векторная форма помогает легче понять, как амплитуда и фаза влияют на гармонические колебания. Этот графический метод особенно полезен при анализе и проектировании радиотехнических систем, где важно визуально представить, как сигналы взаимодействуют между собой.
Проецирование вектора на вертикальную ось
Проецирование вектора на вертикальную ось, осуществляемое через определенные интервалы времени, преобразует вращательное движение вектора в линейное и соответствует синусоидальной форме представления сигнала, в то время как колебания, получаемые при проецировании на горизонтальную ось, принимают форму косинусоиды. Эти два сигнала по сути одинаковы, с исключением начальной фазы, сдвинутой на 90° друг относительно друга. Этот фазовый сдвиг делает их ортогональными. Ортогональные сигналы представляют собой особый случай гармонических колебаний и являются взаимозаменяемыми. Для обозначения фазового сдвига на 90° часто используют символ j или i, представляющий вертикальную ось.
В математике эту ось называют «мнимой», горизонтальную — «действительной», а числа, измеренные по этим осям, называют соответственно «мнимыми» и «действительными». Одновременную (алгебраическую) их запись (a + jb) называют комплексным числом. Действительные и мнимые числа между собой сравнивать нельзя, так как они измерены по разным осям, и это учитывается при выполнении с ними математических операций. Например, мнимые числа можно складывать только с мнимыми, а действительные — только с действительными. Для перехода к показательной комплексной форме записи необходимо по проекциям вектора найти его длину и начальное местоположение. Длина соответствует амплитуде колебания и может быть рассчитана по теореме Пифагора:
Um = √(a^2 + b^2)=√(Umcosφ)^2+(Umsinφ)^2
А местоположение определяется начальной фазой
φ = arctg(b/α)
Если два вектора, соответствующие двум колебаниям, вращаются с одинаковой угловой скоростью, то при определении их взаимодействия вращение векторов можно не учитывать, так как в любой момент времени векторы будут неподвижными относительно друг друга. Однако, если их угловые скорости различны, то для сопоставления колебаний необходимо добавлять компоненты аргумента, учитывающие текущие изменения фазы (ωt), возникающие из-за различия в угловых скоростях вращения.
Как уже подчёркивалось, колебания могут быть изображены как проекции на две перпендикулярные оси. Эта концепция находит своё отражение в их математической форме записи:
u(l)=Umcos(ωl+φ)+jUmsin(ωl+φ)=Umexp[j(ωl+φ)]=Uexp(jωl)
Рассмотрим комплексную амплитуду гармонического сигнала U, которая равна Umexp(jφ). Возможность перехода от алгебраической к показательной форме записи хорошо иллюстрируется. Для этого представим
v = cos(φ) + j sin(φ)
Затем можно рассмотреть производную функции:
dv/dφ = d/dφ (cosφ + jsinφ)=-sinφ+jcosφ=j(cosφ+jsinφ)
то есть
dv/dφ=jv
или
dv/v=jdφ
Итак, для представления гармонического колебания существует несколько равноправных форм записи: тригонометрическая, алгебраическая и показательная. Каждая из них отражает одно и то же колебание, и выбор между ними зависит от удобства применения соответствующего математического инструмента.










