Способы изображения и параметры синусоидальных электрических величин

Введение

В мире электротехники и электроники синусоидальные электрические величины играют ключевую роль. Эти величины представляют собой важный инструмент для анализа и передачи электроэнергии, а также для создания и функционирования различных электрических устройств. Синусоидальные сигналы характеризуются своей уникальной формой и математической структурой, что делает их неотъемлемой частью электротехнических расчетов и проектирования.

В этой статье мы исследуем методы изображения синусоидальных электрических величин и их параметры. Мы рассмотрим математическое описание синусоид и их основных свойств, таких как фаза, амплитуда и частота, а также их взаимосвязь. Кроме того, мы рассмотрим различные методы представления синусоидальных сигналов, такие как фазовые диаграммы и графики, а также их применение в различных областях, таких как связь, электроэнергетика и электроника. В конце концов читатель получит глубокое понимание того, как синусоидальные электрические величины лежат в основе многих аспектов современных технологий и техники.

Почему выбрали синусоидальную форму изменения тока и напряжения?

Синусоидальная форма изменения тока и напряжения выбрана в электрических системах по нескольким причинам:

1. Естественность: Синусоидальные волны являются естественными и наиболее распространенными в природе. Множество физических процессов и колебаний имеют синусоидальную форму. Например, движение колеблющейся пружины или маятника, акустические волны в звуке, электромагнитные волны света и радиоволн — все они могут быть описаны синусоидальными функциями. Поэтому синусоидальные волны естественным образом возникают в электрических системах.
2. Удобство в анализе: Синусоидальные волны обладают рядом математических свойств, которые делают их удобными для анализа и расчетов. Они легко интегрируются, дифференцируются и решаются в уравнениях. Это делает синусоидальную форму удобной для применения в математических моделях и расчетах электрических систем.
3. Устойчивость: Синусоидальные волны являются устойчивыми и неизменными при прохождении через линейные системы. Это означает, что если синусоидальный сигнал проходит через линейное устройство или сеть, его форма остается синусоидальной. Это позволяет легко анализировать и прогнозировать поведение сигнала в различных частях системы.
4. Минимизация гармонических искажений: Синусоидальная форма тока и напряжения минимизирует гармонические искажения в электрических сетях. Гармонические искажения могут вызывать электромагнитные помехи и нежелательные эффекты в системах. Использование синусоидальных сигналов позволяет снизить эти искажения и обеспечить более стабильное электропитание.
5. Совместимость: Множество электрических устройств и аппаратуры разработаны для работы с синусоидальными сигналами. Это создает совместимость между различными компонентами и системами, что упрощает интеграцию и обмен энергией и информацией.

Из-за этих преимуществ синусоидальная форма тока и напряжения стала стандартом для переменного тока в электроэнергетике и электронике.

Основные определения

Синусоидальный электрический ток — это переменный ток, который с течением времени изменяется по гармоническому закону. Синусоидальные величины широко используются в электротехнике, поэтому важно уметь их изображать и анализировать.

График синусоидальной величины — это кривая, которая получается в результате графической зависимости величины от времени.

Таблица синусоидальной величины — это таблица, в которой приведены значения величины для различных моментов времени.

Уравнение синусоидальной величины — это математическое выражение, описывающее зависимость величины от времени.

Параметры синусоидальных величин

• Амплитуда — это наибольшее значение величины.
• Частота — это число полных периодов, совершаемых величиной за единицу времени.
• Период — это время, за которое величина совершает один полный период.
• Начальная фаза — это угол, на который величина сдвинута по фазе относительно начала координат.

Амплитуда — обозначается буквой А. Она измеряется в тех же единицах, что и сама величина.

Частота — обозначается буквой f. Она измеряется в герцах (Гц).

Период — обозначается буквой Т. Он измеряется в секундах (с).

Начальная фаза — обозначается буквой φ. Она измеряется в радианах или градусах.

Преимущества переменного тока

Переменный ток (ПТ) имеет множество преимуществ, которые делают его предпочтительным во многих аспектах электротехники и электроники. Вот некоторые из главных преимуществ переменного тока:

1. Простота трансформации напряжения: ПТ легко преобразуется в различные уровни напряжения с помощью трансформаторов, что делает его удобным для передачи электроэнергии на большие расстояния и обеспечения различных уровней напряжения для различных потребителей.
2. Эффективность передачи: В силу вышеупомянутой возможности трансформации напряжения и тока ПТ, его можно эффективно передавать на длинные расстояния без больших потерь энергии.
3. Простота управления: Возможность легкого регулирования амплитуды и частоты ПТ делает его идеальным для широкого спектра приложений, от освещения до работы электронных устройств.
4. Совместимость с альтернативными источниками энергии: ПТ может быть легко интегрирован с альтернативными источниками энергии, такими как солнечная и ветровая энергия, с минимальными изменениями в инфраструктуре.
5. Экономичность: Системы генерации, передачи и распределения ПТ обычно обходятся дешевле по сравнению с системами постоянного тока (ППТ), и это способствует снижению стоимости производства и потребления электроэнергии.
6. Безопасность: ПТ считается более безопасным для передачи и использования, поскольку его напряжение периодически изменяется, что снижает риск образования долгоживущих дуг и повреждения оборудования.
7. Совместимость с многими устройствами: Множество электрических устройств и моторов работают на переменном токе, и ПТ предоставляет им необходимую форму энергии без дополнительных преобразований.
8. Возможность работы с множеством фаз: ПТ может быть легко создано с различным числом фаз, что позволяет эффективно питать трехфазные системы, широко используемые в промышленности.

Действующее значение переменного тока

Действующее значение переменного тока (RMS, Root Mean Square) — это значение переменного тока, которое имеет ту же эффективную мощность, что и постоянный ток. Оно является способом измерения переменного тока, который позволяет сравнивать его с постоянным током в терминах мощности и относительной интенсивности.

При анализе переменного тока, особенно в электротехнике и электронике, действующее значение переменного тока выражает мощность, которую бы произвело одинаковое количество постоянного тока при том же значении напряжения. Формально, действующее значение переменного тока можно вычислить как квадратный корень из среднего квадрата значений тока за один период.

Для синусоидального переменного тока (который часто встречается в электротехнике), действующее значение равно значению пика тока (максимальному значению) разделенному на корень из 2, что приближенно равно 0,707. Это означает, что значение RMS синусоидального переменного тока равно его пиковому значению умноженному на 0,707.

Действующее значение переменного тока важно при расчетах мощности и эффективности в системах переменного тока, так как оно позволяет учитывать изменяющийся характер тока и напряжения, аналогично постоянному току.

Способы представления гармонических функций

Существует разнообразие методов для отображения гармонических функций.

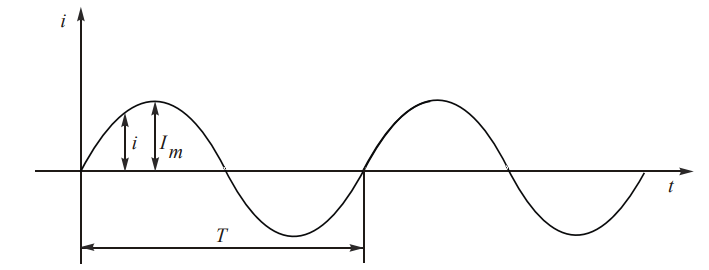
Мгновенное значение переменной величины в определенный момент времени часто обозначают строчными буквами «i,» «u,» или «e.»

По соглашению, наименьший промежуток времени, в течение которого мгновенные значения переменной величины повторяются, называется периодом и обозначается символом «T»:

Период – время одного полного колебания.

Обратную величину периода принято называть частотой и обозначать символом «f»:

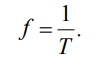
Частота – число полных колебаний в единицу времени:

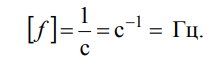
Промышленные частоты электроэнергии в разных странах различаются: в России она составляет 50 Гц, в то время как в США и Японии она равна 60 Гц. Эти частоты были выбраны в прошлом с учетом различных факторов. Нижний предел, равный 50 Гц, определялся требованиями к освещению, чтобы избежать заметных мерцаний света при нулевых значениях тока. В свою очередь, верхний предел, равный 60 Гц, связан с требованиями к скорости вращения валов электродвигателей, которая пропорциональна частоте.

Однако в настоящее время эти значения частоты считаются не самыми оптимальными. Увеличение частоты позволяет снизить вес и габариты электрического оборудования. Однако переход на другую частоту представляет собой сложную задачу, так как это потребует значительных материальных ресурсов и изменений в существующей инфраструктуре.

В некоторых случаях преобразователи частоты используются для решения проблемы с весом и размерами оборудования. Например, для питания оборудования в лесоповалах может использоваться напряжение с частотой 400 Гц. В авиации также часто используются автономные источники электроэнергии с частотами, значительно выше обычных 50 или 60 Гц (несколько тысяч Гц), чтобы уменьшить вес и размеры оборудования, установленного на самолетах.

Изображение тригонометрическими функциями

Мгновенные значения электрических величин являются синусоидальными функциями времени:

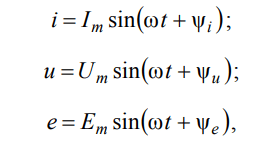
Мгновенные значения электрических величин, обозначаемые как i, u и e, представляют текущие значения этих величин в конкретный момент времени.

Максимальные (амплитудные) значения, обозначаемые как E, U и I, представляют максимальные значения этих величин в течение одного периода синусоидальной функции времени.

Фаза колебания

Обозначаемая как (ωt + ψ), определяет положение синусоидальной функции в определенный момент времени. Где ω — угловая частота, t — текущее время, ψ — начальная фаза.

Текущий угол

ωt – текущий угол, который отсчитывают от начала отсчета времени. Этот угол отсчитывается в радианах и зависит от текущего времени t и угловой частоты ω. Угловая частота ω определяет скорость изменения фазы с течением времени и связана с частотой f следующим образом: ω = 2πf, где 2π — это полный угол в радианах.

Угловая циклическая частота

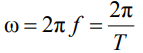
Угловая циклическая частота (ω) определяет скорость изменения фазы в синусоидальной функции. Она измеряется в радианах в секунду и связана с обычной частотой (f) через выражение ω = 2πf.

Начальная фаза (ψ) представляет угол, который определяет значение синусоидальной функции в момент времени t = 0, и важна для определения её начального положения.

Представления гармонических функций

Начальная фаза может быть положительной и отрицательной. У синусоиды, на изображении выше, начальная фаза ψ = 0 .

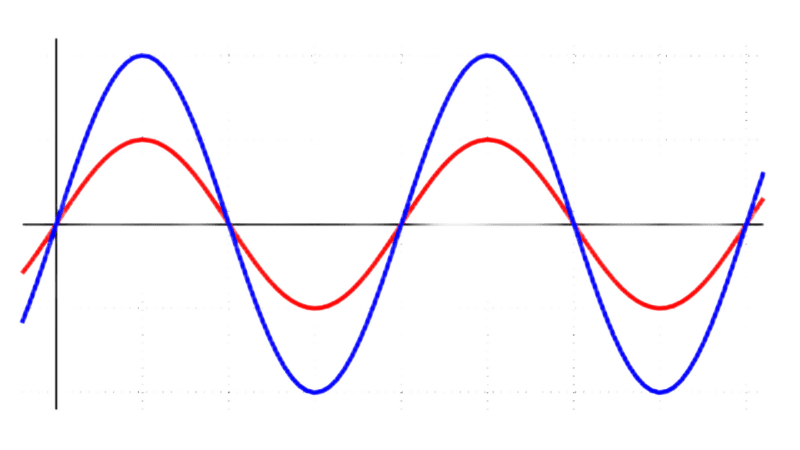
Положительную начальную фазу откладывают влево от начала координат (см. ток i1 на изображении ниже), отрицательную – вправо (см. ток i2).

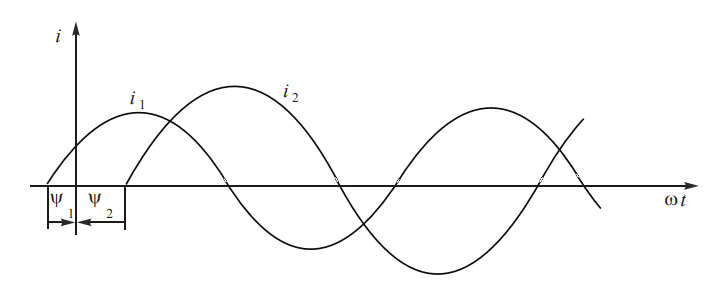
Имеется постоянный фазовый сдвиг между токами i1 и i2, который сохраняется при заданных начальных фазах. Угол сдвига между фазой напряжения и током, выраженный как ψu — ψi, представляет собой одну из ключевых характеристик электрической цепи. Если значение угла α равно нулю, это указывает на совпадение фаз между напряжением и током.

Изображение вращающимися векторами

Проведение математических операций с синусоидальными величинами может быть сложным. Однако их можно представить как вращающийся вектор с угловой скоростью ω, что упрощает анализ и вычисления. Этот метод широко используется в электротехнике и электронике для работы с синусоидальными сигналами.

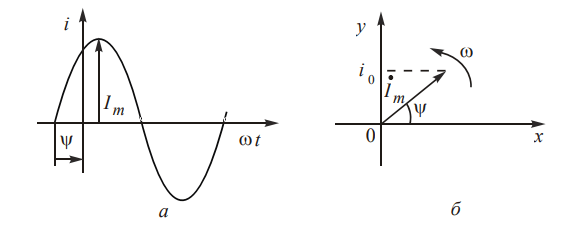
В начальный момент времени (t = 0), вектор изображается как V(0). Фаза колебания (ωt + ψ) в этот момент времени равна ψ. Длина вектора в масштабе представляет амплитудное значение величины. Вращающиеся векторы обозначаются заглавной буквой с точкой над ней, например, V̇.

Вертикальная проекция вектора определяет мгновенное значение тока при t = 0: i0 = Im sin ψ. При вращении с одинаковой скоростью, все векторы остаются взаимно неподвижными. Совокупность векторов, отображающих процесс в цепи, называется векторной диаграммой. Применение вращающихся векторов позволяет заменить тригонометрические и графические операции над мгновенными значениями действиями над вращающимися векторами. Однако следует отметить, что векторные диаграммы предоставляют только графическое решение задачи.

Изображение комплексными числами

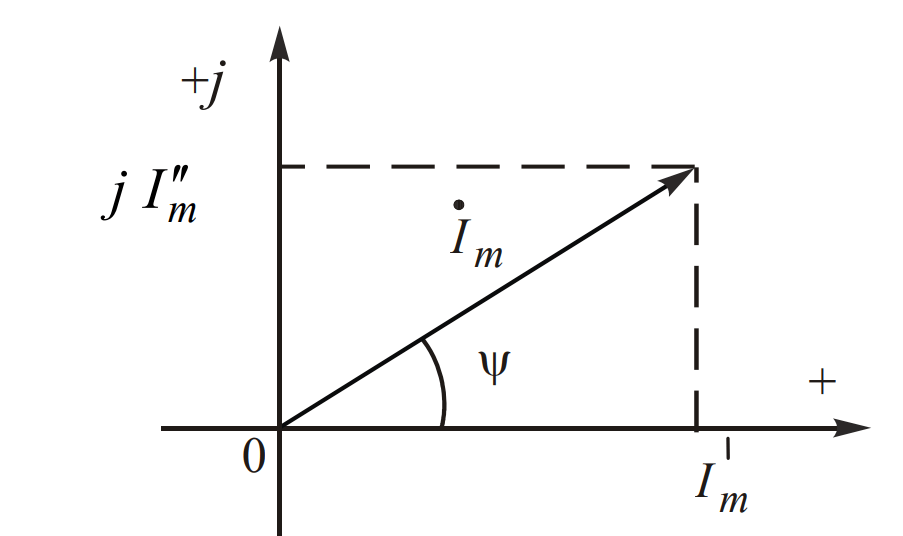
Для аналитического решения, мы можем заменить плоскость координат XOY комплексной плоскостью.

Так как буквой i в электротехнических дисциплинах обозначают ток, то мнимую единицу обозначают буквой

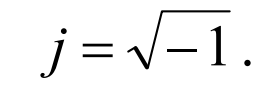
Вектору на комплексной плоскости можно сопоставить комплексное число:

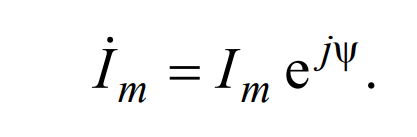
На комплексной плоскости, комплексное число представляется модулем Im и аргументом ψ. Эту форму записи чисел принято называть показательной. Это удобно использовать при умножении и делении комплексных чисел, так как позволяет упростить алгебраические операции с ними.

Для сложения и вычитания комплексных чисел в показательной форме необходимо перейти к алгебраической форме. Это можно сделать, разложив вектор на проекции по осям координат: действительную (Im’) и мнимую (Im») части, где Im = Im’ + jIm».

Переход от одной формы записи к другой делают по формулам, полученным из решения треугольника:

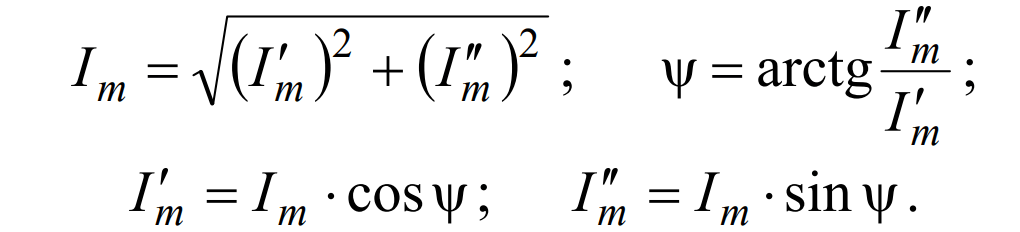
Метод расчета цепей синусоидального тока при помощи комплексных чисел называют символическим.

Действующие и средние значения гармонических величин

Действующие значения

Сравнивая синусоидальный и постоянный токи, оценивают тепловое действие. Постоянный ток подбирается так, чтобы за одинаковое время выделялось одинаковое количество тепла:

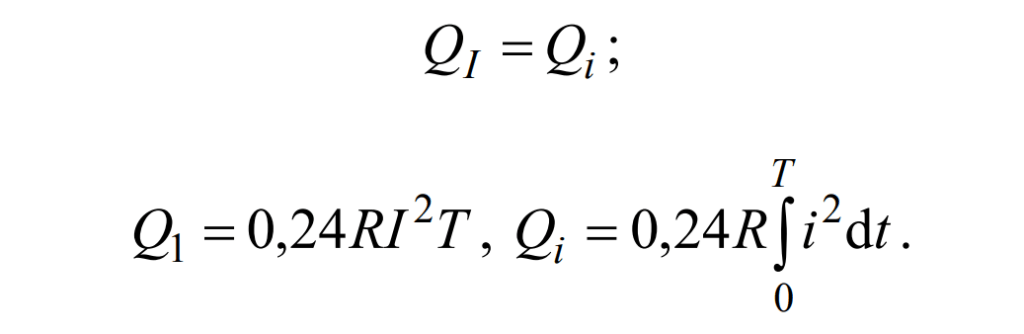
Отсюда следует

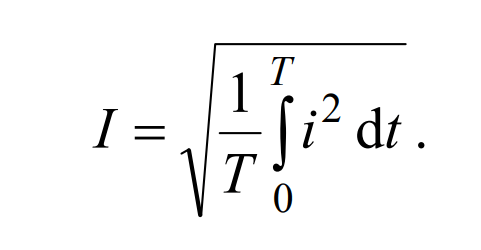
Действующим значением тока считают такой постоянный ток, который производит тот же тепловой эффект, что и реальный переменный ток.

Примем начальную фазу ψi для простоты равной нулю. Тогда i = Im sinωt .

Действующее значение тока:

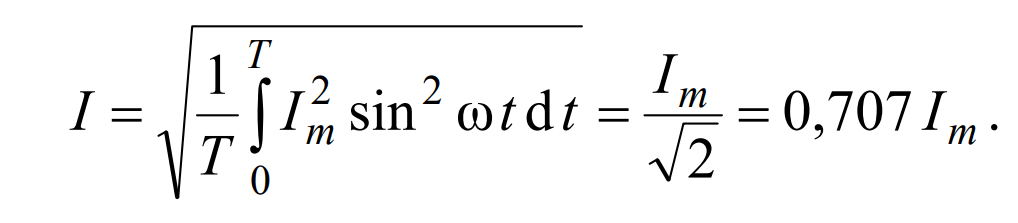
Аналогично

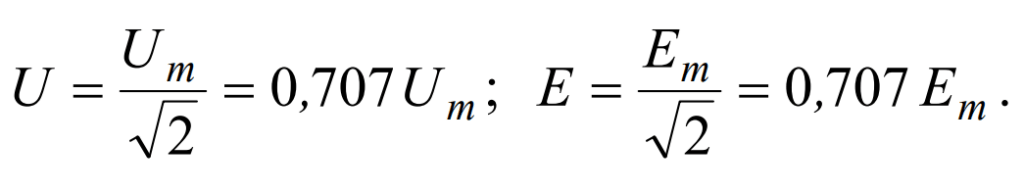
Поскольку воздействие переменного тока характеризуется действующими значениями, векторные диаграммы обычно представляют векторы действующих, а не максимальных значений. Действующие значения токов и напряжений измеряются амперметрами и вольтметрами электромагнитных и электродинамических систем. Этот подход позволяет более точно оценить воздействие переменного тока на электрические цепи и устройства.

Средние значения

В общем случае, среднее значение обычно определяется как среднее значение за один период (полный цикл).

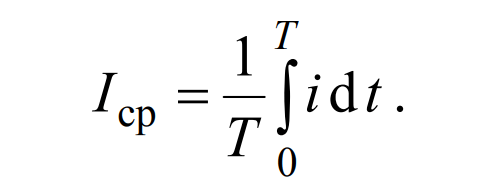
Это среднее значение может использоваться для оценки характеристик переменных величин, таких как напряжение или ток, которые изменяются во времени и имеют периодический характер. Среднее значение за период помогает учесть изменения величины в течение всего цикла и представляет собой полезную характеристику для анализа переменных сигналов.

Для синусоидальных величин, среднее значение за один полный период действительно равно нулю. Поэтому для определения среднего значения синусоидальной величины учитывается только половина периода (или полупериод):

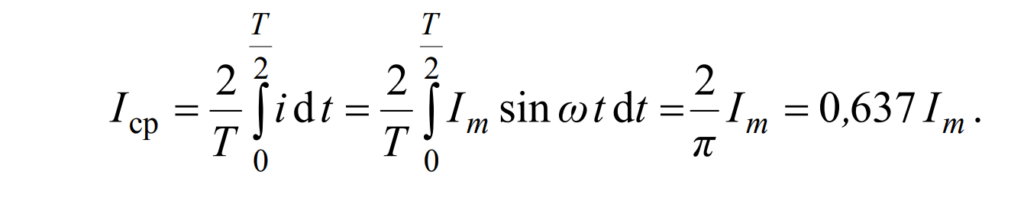
И аналогично

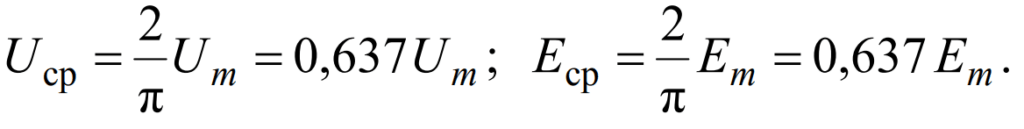
Связь максимального и действующего значения синусоидальных электрических величин

Максимальное (пиковое) значение и действующее (RMS) значение синусоидальных электрических величин связаны следующим образом:

1. Максимальное (пиковое) значение (I_peak или V_peak): Это значение представляет максимальную амплитуду синусоидальной величины. Для тока это означает максимальное значение тока, а для напряжения — максимальное значение напряжения в колебаниях. Например, для стандартной синусоидальной волны, максимальное значение тока или напряжения соответствует точке на графике в самом верхнем или нижнем положении.
2. Действующее (RMS) значение (I_RMS или V_RMS): Это значение представляет корень из среднего квадрата (среднеквадратичное значение) синусоидальной величины за один период. Оно является мерой эффективной мощности, которую бы произвело соответствующее постоянное значение тока или напряжения. Для стандартной синусоидальной волны действующее значение тока или напряжения примерно равно 0,707 (или точно 1/√2) раз максимального значения.

Связь между максимальным и действующим значениями синусоидальных электрических величин выражается следующим образом:

• I_RMS = I_peak / √2
• V_RMS = V_peak / √2