Глубокий Взгляд в Мир X-Конденсаторов

Введение

X-конденсаторы представляют собой важный элемент в мире электроники, играющий ключевую роль в обеспечении стабильности и безопасности электрических систем. Эти уникальные компоненты обладают специфическими характеристиками, делая их незаменимыми в различных электрических устройствах. Однако, чтобы полностью понять и оптимизировать их функциональность, необходимо обратиться к математике, которая является ключом к разгадыванию их электрических тайн.

Определение X-конденсаторов

X-конденсаторы — это конденсаторы, которые используются для подавления помех в цепях переменного тока, например, в блоках питания, зарядных устройствах, светильниках и др. X-конденсаторы подключаются параллельно к сетевому напряжению и обеспечивают фильтрацию дифференциальных помех, то есть помех, возникающих между фазой и нулем. X-конденсаторы должны иметь высокую диэлектрическую прочность, низкий тангенс угла потерь и высокую стабильность ёмкости.

X-конденсаторы получили свое название из-за символа «X», который обозначается на их корпусе. Они являются одним из трех классов конденсаторов, определенных в стандарте IEC 60384-14, где каждый класс имеет свои характеристики и предназначение.

Основной целью X-конденсаторов является фильтрация помех, создаваемых в электроэнергетической сети, таких как высокочастотные импульсы, электромагнитные воздействия и другие возмущения переменного тока. Это позволяет обеспечивать более стабильное и надежное электропитание для подключенных устройств.

Обозначение на электрической схеме

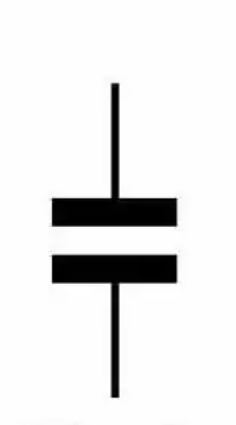
На электрической схеме X-конденсаторы обозначаются стандартным символом: две параллельные линии, разделенные прерывистой линией. Этот символ указывает на их способность хранить электрическую энергию и их роль в сглаживании напряжения в электрических цепях.

Основы X-Конденсаторов

X-конденсаторы представляют собой важный класс электронных компонентов, обладающих уникальной структурой и характеристиками, что делает их ключевыми для эффективной фильтрации помех в электронных схемах.

Структура X-Конденсаторов:

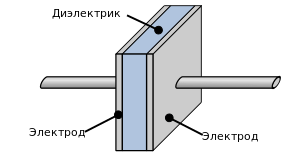
X-конденсаторы имеют конструкцию, призванную обеспечить высокий уровень изоляции и устойчивость к переменному току. Основные элементы структуры включают:

1. Две Изолированные Части: X-конденсаторы часто состоят из двух отдельных частей, разделенных диэлектриком. Это позволяет им создавать эффективный барьер между цепями переменного тока и электронными устройствами, к которым они подключены.
2. Диэлектрик Высокой Изоляции: Одним из ключевых элементов является диэлектрик, который имеет высокий коэффициент изоляции. Это обеспечивает эффективную блокировку переменного тока и защиту от помех.
3. Электроды и Пластины: X-конденсаторы имеют два электрода, обычно выполненных из металла, и пластины, расположенные между электродами и диэлектриком. Эти элементы играют решающую роль в емкостных и электрических характеристиках конденсатора.

Основные Характеристики X-Конденсаторов:

1. Емкость (С): Определяет количество электрического заряда, которое X-конденсатор может хранить при заданном напряжении.
2. Напряжение (U): Максимальное напряжение, которое X-конденсатор может выдерживать без разрыва.
3. Частотная Характеристика: Учитывает, как изменение частоты воздействующего переменного тока влияет на характеристики X-конденсатора.

Роль Математики в Анализе и Проектировании:

Математика играет ключевую роль в анализе и проектировании X-конденсаторов по следующим причинам:

1. Математическое Моделирование: Математические модели позволяют описать электрические характеристики X-конденсаторов, что важно для предсказания их поведения в различных условиях.
2. Оптимизация Ёмкости и Напряжения: Математический анализ позволяет оптимизировать параметры конденсатора, такие как емкость и напряжение, с учетом требований конкретного применения.
3. Частотные Расчеты: Математика необходима для анализа воздействия переменного тока на X-конденсатор и определения его частотных характеристик.

Использование математики в анализе и проектировании X-конденсаторов обеспечивает точное моделирование и оптимизацию их характеристик, что является важным элементом в создании надежных и эффективных электронных систем.

Математическая Модель Работы X-Конденсаторов

Математический анализ электрических характеристик X-конденсаторов играет критическую роль в понимании и оптимизации их работы. Разберем основные математические уравнения и принципы, описывающие поведение X-конденсаторов.

Емкость X-Конденсатора (C)

Емкость X-конденсатора определяется классическим уравнением:

Q = C \cdot U

где

• Q — электрический заряд
• C — емкость конденсатора
• U — напряжение на конденсаторе.

Это уравнение позволяет определить количество заряда, которое X-конденсатор способен хранить при заданном напряжении.

Реактивное Сопротивление (Xc)

X-конденсаторы имеют реактивное сопротивление, зависящее от частоты переменного тока. Для анализа этого параметра используется уравнение:

X_c = \frac{1}{2\pi fC}

где

• Xc — реактивное сопротивление
• f — частота переменного тока
• C — емкость конденсатора.

Это уравнение отражает, как реактивное сопротивление X-конденсатора изменяется в зависимости от частоты внешнего воздействия.

Угловая Частота (ω)

Угловая частота связана с частотой переменного тока следующим уравнением:

\omega = 2\pi f

где

• ω — угловая частота
• f — частота переменного тока.

Угловая частота используется в дальнейших математических моделях для анализа динамических характеристик X-конденсаторов.

Комплексная Емкость (Z)

Используя угловую частоту, комплексная емкость X-конденсатора может быть выражена как:

Z = \frac{1}{j\omega C}

где

• Z — комплексное сопротивление
• j — мнимая единица.

Это уравнение позволяет представить реактивное сопротивление в комплексной форме, что является основой для анализа электрических характеристик в различных условиях переменного тока.

Поведение при Различных Частотах

Математические модели позволяют анализировать поведение X-конденсаторов при различных частотах переменного тока. При низких частотах X-конденсатор имеет высокое реактивное сопротивление, что делает его эффективным для фильтрации низкочастотных помех. При повышении частоты, реактивное сопротивление уменьшается, что обеспечивает устойчивость работы на более высоких частотах.

Математика в данном контексте предоставляет инструменты для точного моделирования и предсказания электрических характеристик X-конденсаторов при различных условиях. Это позволяет инженерам оптимизировать их использование в электронных схемах и обеспечивать стабильность и надежность работы устройств в различных сценариях.

Функции и Применение X-Конденсаторов

Фильтрация Высокочастотных Помех:

• Функция:
  • X-конденсаторы выполняют функцию фильтрации высокочастотных помех, предоставляя низкое реактивное сопротивление на высоких частотах.
• Формула:
  • Реактивное сопротивление (Xc) обратно пропорционально частоте (f):

X_c = \frac{1}{2\pi fC}

Изоляция Между Цепями:

• Функция:
  • Создание эффективного барьера между цепями переменного тока и устройствами, обеспечивая изоляцию.
• Формула:
  • Изоляция реализуется высокой емкостью (C) и напряжением (U).

Подавление Низкочастотных Возмущений:

• Функция:
  • Устранение низкочастотных помех, обеспечивая стабильность работы электронных систем.
• Формула:
  • Низкое реактивное сопротивление при низких частотах.

Стабилизация Напряжения:

• Функция:
  • Поддержание стабильного уровня напряжения в электрических схемах.
• Формула:
  • Зависимость емкости (C) от напряжения (U) в уравнении заряда конденсатора.

Примеры Приложений и Формул для Анализа

Источники Питания:

• Применение:
  • X-конденсаторы используются в источниках питания для фильтрации шумов переменного тока.
• Формула:
  • Реактивное сопротивление (Xc) определяется частотой (f) и емкостью (C).

Инверторы переменного тока (UPS):

• Применение:
  • Обеспечение стабильности напряжения и изоляции от сетевых помех.
• Формула:
  • Используется уравнение комплексной емкости для анализа динамических характеристик.

Z = \frac{1}{j\omega C}

Электронные Блоки Питания:

• Применение:
  • Гарантирование чистого электропитания для устройств.
• Формула:
  • Работа на различных частотах (f) учитывается при анализе эффективности.

Источники Питания для Медицинского Оборудования:

• Применение:
  • Обеспечение стабильного электропитания для медицинских устройств.
• Формула:
  • Расчет реактивного сопротивления (Xc) для заданных условий.

Математические Аспекты Разработки X-Конденсаторов

Влияние Математики на Процесс Проектирования X-Конденсаторов:

Математическое Моделирование:

• Влияние: Математика позволяет создавать математические модели, описывающие электрические характеристики X-конденсаторов.
• Применение: Это позволяет инженерам предсказывать поведение конденсаторов в различных условиях и подбирать оптимальные параметры.

Определение Ёмкости и Напряжения:

• Влияние: Математические уравнения связывают емкость и напряжение, определяя их влияние на общую производительность.
• Применение: Это важно при выборе параметров для конкретных приложений и обеспечивает соответствие требованиям стандартов.

Частотные Расчеты:

• Влияние: Математика используется для анализа зависимости реактивного сопротивления от частоты, что определяет эффективность конденсатора при различных частотах.
• Применение: Позволяет выбирать конденсаторы, которые наилучшим образом соответствуют частотам переменного тока в конкретном приложении.

Оптимизация Диэлектрика:

• Влияние: Математическое моделирование позволяет оптимизировать свойства диэлектрика, учитывая различные материалы и их характеристики.
• Применение: Обеспечивает выбор материала для диэлектрика, который обеспечивает наилучшую изоляцию при заданных условиях.

Оптимизация Параметров с Использованием Математических Методов:

Методы Оптимизации:

• Применение: Инженеры используют математические методы оптимизации, такие как метод наименьших квадратов или генетические алгоритмы, чтобы находить оптимальные значения параметров X-конденсаторов.

Анализ Чувствительности:

• Применение: Математический анализ чувствительности позволяет определить, как изменения в каждом параметре влияют на общую производительность конденсатора. Это помогает выявить критические параметры, которые нуждаются в особенном внимании.

Системы Уравнений:

• Применение: Решение систем уравнений, описывающих электрические характеристики X-конденсаторов, является ключевым шагом в оптимизации параметров. Математика позволяет эффективно решать сложные системы уравнений.

Моделирование Работы в Различных Условиях:

• Применение: Использование математических моделей для моделирования работы X-конденсаторов при различных температурах, влажностях, и других условиях помогает предвидеть их поведение в реальных условиях эксплуатации.

Математическое Моделирование Шумов и Импульсов в Работе X-Конденсаторов

Воздействие Электромагнитных Шумов:

• Моделирование:
  • Математическое моделирование воздействия электромагнитных шумов на X-конденсаторы может быть основано на уравнениях, описывающих передачу электромагнитных волн в электрических цепях.
• Формула для Реакции на Шум:
  • Реакция на электромагнитный шум может быть оценена через изменение реактивного сопротивления (Xc) с увеличением частоты шума.
• Пример:
  • Уравнение изменения реактивного сопротивления:

X_c = \frac{1}{2\pi fC}

Воздействие Импульсных Напряжений:

• Моделирование:
  • Для моделирования воздействия импульсных напряжений на X-конденсаторы используются уравнения, описывающие динамику изменения напряжения и емкости в ответ на импульс.
• Формула для Оценки Стабильности:
  • Оценка стабильности работы X-конденсатора в ответ на импульс может включать в себя уравнения, учитывающие изменение напряжения и емкости.
• Пример:
  • Уравнение изменения напряжения в ответ на импульс:

\Delta U = \frac{\Delta Q}{C}

Оценка Уровня Шума:

• Моделирование:
  • Математическое моделирование уровня шума в X-конденсаторах может быть выполнено с использованием статистических методов, таких как анализ шумовых спектров.
• Формула для Оценки Шума:
  • Оценка уровня шума может включать в себя уравнения для вычисления шумового напряжения или тока.
• Пример:
  • Уравнение для оценки шума в напряжении:

 V_{\text{шум}} = \sqrt{\int_{f_{\text{min}}}^{f_{\text{max}}} S_V(f) \,df}

Моделирование Импульсных Напряжений:

• Моделирование:
  • Импульсные напряжения можно моделировать с использованием уравнений, описывающих форму и параметры импульсов.
• Формула для Моделирования Импульса:
  • Уравнение формы импульса может включать параметры, такие как амплитуда, длительность и форма волны.
• Пример:
  • Уравнение для импульса прямоугольной формы:

V(t) = V_0 \cdot \text{rect}\left(\frac{t}{\tau}\right)

Эксперименты и Практические Примеры с X-Конденсаторами

1. Электромагнитные Шумы: Понимание Чувствительности X-Конденсаторов:

• Цель: Изучение, как X-конденсаторы реагируют на электромагнитные шумы в электрических цепях.
• Эксперимент: Подключите X-конденсатор к источнику переменного тока с известным уровнем шумов. Измерьте изменения в его реактивном сопротивлении при различных частотах шумов.
• Результат: Определение, какие частоты электромагнитных шумов наиболее влияют на работу X-конденсаторов.

2. Фильтрация Шумов в Источнике Питания: Практическое Применение:

• Цель: Проектирование и проверка эффективности X-конденсатора в фильтрации шумов в источнике питания.
• Эксперимент: Подключите X-конденсатор параллельно источнику питания и измерьте уровень шумов на выходе. Оцените, насколько X-конденсатор уменьшает шумы.
• Результат: Оценка практического влияния X-конденсатора на чистоту электропитания.

3. Оценка Стабильности при Импульсных Напряжениях:

• Цель: Понимание поведения X-конденсатора при воздействии импульсных напряжений.
• Эксперимент: Примените импульсное напряжение разной силы и длительности к X-конденсатору, измерьте изменения напряжения и емкости.
• Результат: Оценка устойчивости X-конденсатора при различных импульсных воздействиях.

4. Пример Использования X-Конденсатора в Инверторе:

• Цель: Рассмотрение роли X-конденсатора в инверторе переменного тока.
• Эксперимент: Интегрируйте X-конденсатор в цепь инвертора переменного тока, измерьте уровень шумов и стабильность выходного напряжения.
• Результат: Понимание, как X-конденсатор влияет на чистоту выходного напряжения и стабильность работы инвертора.

Эти примеры помогают в живом формате продемонстрировать важность и эффективность X-конденсаторов в реальных сценариях их использования.

Инновации в Мире X-Конденсаторов

В последнее время отмечаются значительные передвижения в сфере X-конденсаторов, где инновации, подкрепленные математическими исследованиями, перерисовывают картину их применения и эффективности.

Такие новаторские подходы включают в себя:

Материалы Диэлектрика:
Новые материалы диэлектрика с улучшенными электрическими свойствами, ставшие результатом математического моделирования, сфокусированного на анализе и предсказании их воздействия на характеристики X-конденсаторов.

Технологии Производства:
Интеграция высокотехнологичных методов, таких как нанотехнологии, в производственные процессы, улучшая точность и эффективность конструкции X-конденсаторов с помощью математического моделирования.

Работа при Низких Температурах:
Разработка X-конденсаторов, способных функционировать в условиях экстремальных низких температур, предшествовавшая математическому моделированию тепловых процессов.

Интеллектуальные Системы Управления:
Интеграция X-конденсаторов с интеллектуальными системами управления, адаптивно оптимизирующими параметры в реальном времени, с использованием математических моделей для предвидения динамических изменений.

Хранение Энергии:
Тенденция к повышению эффективности X-конденсаторов в качестве устройств для хранения энергии, поддерживаемая математическим моделированием процессов зарядки и разрядки.

Прогнозы для Будущего Развития X-Конденсаторов:

Интеграция в IoT:
Эволюция X-конденсаторов с учетом требований Интернета вещей, ориентированная на обеспечение стабильности и эффективности электронных устройств, соответственно разрабатываемая с использованием математических моделей.

Энергоэффективные Технологии:
Создание энергоэффективных X-конденсаторов, способных эффективно обеспечивать стабильность электропитания, с учетом различных режимов использования, оптимизируемых через математическое моделирование.

Заключение о X-конденсаторах

В современном мире X-конденсаторы не просто электронные компоненты — они становятся центром инноваций и технологического прогресса. Их эволюция, поддерживаемая математическими исследованиями, приводит к существенным улучшениям в дизайне и функциональности.

Новые материалы диэлектрика, разработанные с использованием математических моделей, улучшают емкость и стабильность X-конденсаторов. Технологии производства, оптимизированные с помощью математического подхода, делают их более точными и эффективными. Работа при низких температурах, интеграция с умными системами управления и энергосберегающие решения расширяют их применение.

Прогнозы для будущего говорят о более тесной интеграции в мир Интернета вещей и создании более энергоэффективных устройств. Таким образом, X-конденсаторы, подкрепленные математикой, представляют собой не только ключевой элемент электроники, но и источник бесконечных возможностей для инноваций и усовершенствований в области современных технологий.